Julián nos introduce el punto de vista de los “Juegos matemáticos”, creando un interesante debate. ¿Cuáles de nuestras inversiones tienen esperanza matemática de crecimiento y cuáles son solo apuestas en un casino?

La inversión y los juegos de suma cero. Por Julián Guirao

En teoría de juegos se conocen como “juegos de suma cero” aquellos en los que la suma total de los beneficios y pérdidas de todos los participantes es igual a cero. Es decir, lo que ganan unos participantes es igual a lo que pierden otros y viceversa. No existe creación de valor desde una perspectiva general. Lo opuesto son los juegos de suma no nula, en los que sí existe una ganancia (o pérdida) neta de valor.

Quizás esta explicación queda un poco abstracta, veamos algunos ejemplos de juegos de suma cero para entender mejor el concepto: una partida de poker con los amigos entraría en esta categoría, el ganador de la partida se lleva el dinero que todos los demás han perdido. Otro ejemplo son las apuestas de todo tipo como loterías, quinielas, casinos, etc., en las que todos los participantes ponen un poco de dinero que acaban repartiéndose unos pocos ganadores.

Cierto es que en el último ejemplo no he tenido en cuenta los impuestos ni las comisiones de los intermediarios. Mi intención es tratar este tema desde un punto de vista más teórico que práctico, intentando simplificar al máximo para que se entienda de forma sencilla. Si entramos en detalle los casos pueden ser muy variados y acabamos analizando situaciones muy concretas, por lo tanto seguiremos sin tener en cuenta los impuestos y comisiones en el resto del artículo. Echter, hay que tener muy presente que en el mundo real si existen, y que convierten todos los juegos de suma cero en negativa, donde los beneficios netos de los ganadores no compensan las pérdidas de los demás y, por lo tanto, hay más probabilidad de perder que de ganar.

¿Pero esto qué tiene que ver con la bolsa y las inversiones? Toda inversión se puede considerar como un juego de suma cero, de suma positiva o de suma negativa. Invertir en un negocio que funcione, como un bar, puede verse como un juego de suma positiva. El primer propietario monta el negocio gastando una cantidad determinada de dinero, con el que recibe unos ingresos mensuales. Al traspasarlo a un segundo propietario le pedirá (en condiciones normales) el mismo dinero o un poco más de lo que le costó abrir el bar, y esta persona tendrá también unos ingresos mensuales. Y el tercero, y el cuarto… Como se puede ver en este sencillo ejemplo, todos los participantes ganan dinero, incluso aunque el traspaso fuera siempre por la misma cantidad, ya que reciben unas rentas mensuales mientras conservan el negocio.

¿Es la bolsa un juego de suma cero?. En mi opinión no lo es, siempre y cuando se den tres premisas:

• que las inversiones sean a largo plazo
• que se concentren en empresas estables y con beneficios recurrentes
• que las compras se hagan a buen precio (no me refiero a baratas, sino a un precio justo que proporcione un retorno adecuado, huyendo de las valoraciones desorbitadas).

Al comprar acciones siguiendo las premisas anteriores, estamos adquiriendo negocios que funcionan, como en el ejemplo del bar, de los cuales obtendremos unas rentas (dividendos) y/o venderemos a un precio superior. Esto es así porque las empresas generan valor para los propietarios, tal y como se puede ver en cualquier gráfico de bolsa de largo plazo (jaar oud) que tenga en cuenta los dividendos repartidos. Son gráficos que siempre suben, y cuyos participantes pueden ganar sin que haya perdedores. En la imagen inferior se muestra un ejemplo sobre el índice DAX, que incluye los dividendos repartidos, en el cual se han elegido 4 periodos de 10 años para evitar los ciclos económicos. Como se puede apreciar, en todos estos ciclos ha habido una rentabilidad total positiva de entre el 65% en 140%.

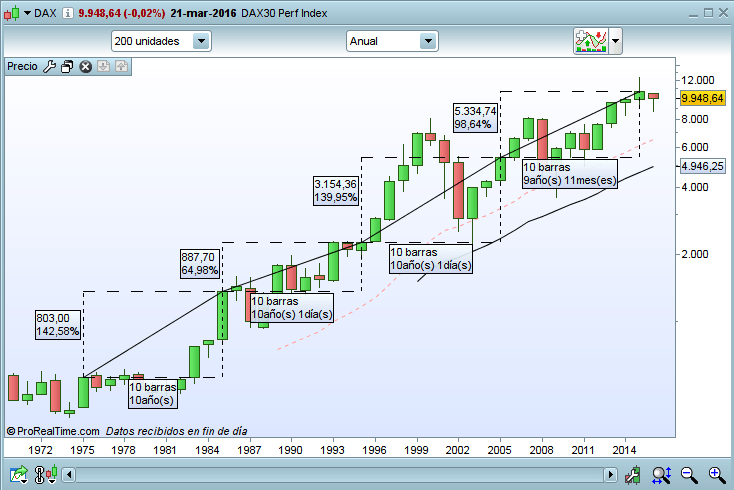
He hablado de la compra de acciones porque otros tipos más o menos habituales de inversión sí son juegos de suma cero. Buscando ejemplos nuevamente tenemos el trading de corto plazo (trading es cuando compramos y vendemos acciones en cuestión de días, horas e incluso minutos), en el que los beneficios de unos inversores compensan las pérdidas de otros y no hay generación de valor, dado que no da tiempo a que las empresas que se compran y se venden generen beneficios significativos. También la inversión en derivados como opciones, futuros o CDFs son juegos de suma cero. En el caso de las opciones las primas que se ingresan o se pagan se compensan y acaban sumando cero. En futuros y CDFs siempre existe una contrapartida con la posición contraria que equilibra el sistema.

Entonces, ¿es imposible ganar o invertir bien en juegos de suma cero? No es imposible, pero hay que tener muy en cuenta al contrincante que, conscientemente, adopta una posición contraria a la nuestra pensando que es ganadora. La única forma de ganar es formarse y obtener experiencia antes de pretender ganar dinero en los juegos de suma cero (trading, CDFs, VIX, opciones…), en los que nuestros oponentes son personas muy preparadas y que se ganan la vida con ello. Justo como sucede en las partidas de poker, a nadie se le ocurriría sentarse a jugar sin saberse las reglas, o apostar todo su patrimonio sin tener experiencia. Pudiendo elegir entre todas las alternativas existentes, quizás lo más prudente es buscar los juegos de suma positiva, como las estrategias Buy & Hold o Value, donde las probabilidades de ganar juegan a nuestro favor, al menos mientras nuestras habilidades no sean suficientes para ser los vencedores en la partida de trading.
Y ya me despido con la esperanza de que os haya resultado interesante esta reflexión. No quiero que nadie se quede con la conclusión de que todos los derivados son peligrosos por igual ni todas las estrategias tienen las de perder. He metido todas estas alternativas en el mismo saco por su naturaleza de ser juegos de suma cero desde un punto de vista matemático, pero usados de manera adecuada pueden ser muy interesantes incluso para el inversor promedio, sobre todo las opciones financieras. Si tiene buena acogida entre los lectores, este tema da para ampliar con futuros artículos. Con permiso del creador del blog, cursus.